Brusselator

Le modèle du Brusselator est un modèle théorique proposé par Ilya Prigogine et ses collaborateurs de l'université libre de Bruxelles. Ce modèle est utilisé pour décrire un type de réaction autocatalytique, c'est-à-dire dont un des produits catalyse la réaction.

Modélisation

Le modèle du Brusselator est caractérisé par ce type de réactions :

A\rightarrow X

2X Y\rightarrow 3X

B X\rightarrow Y D

X\rightarrow E

Dans les conditions où les espèces chimiques A et B seraient en excès massif et dont les concentrations peuvent ainsi être modélisées comme constantes au cours du temps, l'équation cinétique devient alors le système suivant :

{\mathrm {d}  \over \mathrm {d} t}\left\{X\right\}=\left\{A\right\} \left\{X\right\}^{2}\left\{Y\right\}-\left\{B\right\}\left\{X\right\}-\left\{X\right\}

{\mathrm {d}  \over \mathrm {d} t}\left\{Y\right\}=\left\{B\right\}\left\{X\right\}-\left\{X\right\}^{2}\left\{Y\right\}

dans lequel, pour plus de commodité, les constantes cinétiques ont été fixées à 1.

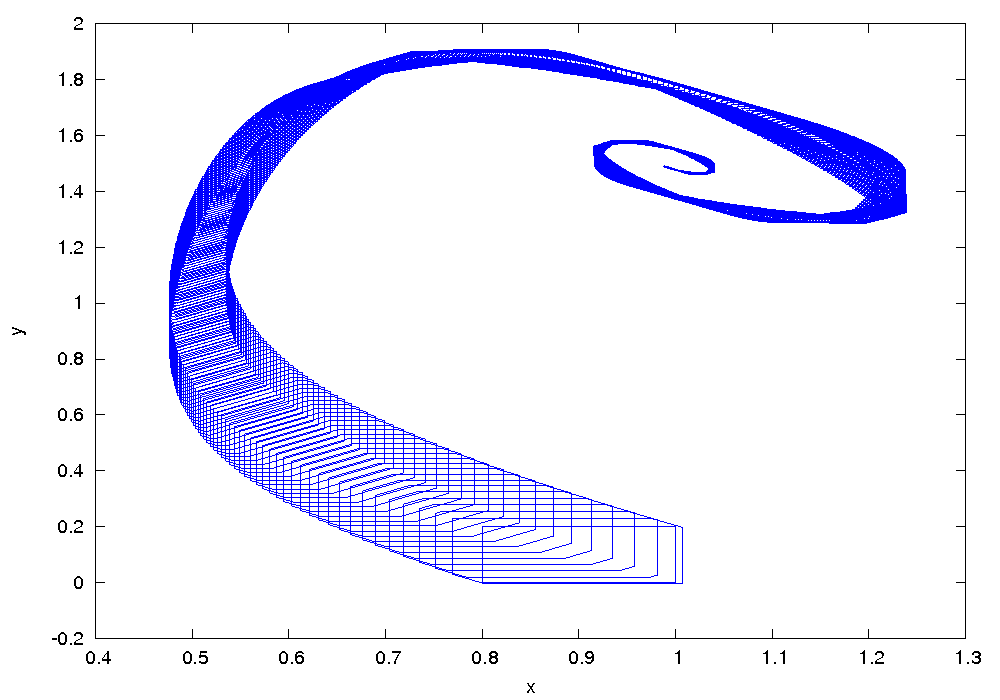
Le modèle du Brusselator présente un état limite du système :

\left\{X\right\}=A

\left\{Y\right\}={B \over A}

L'état limite du système devient instable si :

B>1 A^{2}

ce qui conduit à une oscillation du système.

À la différence du système d'équations différentielles de Lokta-Volerra, les oscillations du modèle de Brusselator ne dépendent pas de la quantité de réactif initialement présent. Au contraire, après un délai suffisant, les oscillations convergent vers un cycle limite.

L'exemple le plus connu est une réaction oscillante : la réaction de Belooussov-Jabotinski (dite BZ). Cela peut être créé à partir d'un mélange de bromate de potassium (KBrO₃), d'acide malonique (CH₂(COOH)₂) et de sulfate de manganèse(II) (MnSO₄), dans une solution chauffée d'acide sulfurique (H₂SO₄).